Analyse de Fourier
Vous êtes ici : Audio >Apprendre
English Version...
English Version...

Du mathématicien Joseph FOURIER (18ème siècle) à ne pas confondre avec Charles FOURIER (même époque mais théoricien du "Fouriérisme", ancêtre du "Communisme").
En gros, Joseph démontre que tout son MUSICAL (donc pas les bruits), COMPLEXE (donc pas simple), de fréquence F, peut être décomposé en une addition de sons SIMPLES (sinusoïde : son produit par un simple oscillateur, un beep) et de ses HARMONIQUES de fréquences 2F puis 3F, 4F, etc....
Autrement dit, si on joue un La2 sur un orgue, il est composé :
- de beaucoup de La 2 simple, la fondamentale, fréquence F soit 220 Hz
- d'un peu de La 3 simple, la 1ère harmonique, l'octave : fréquence 2F soit 440 Hz, ce qui donne après addition
- d'un peu de Mi 4 simple, la 2ème harmonique, la quinte : fréquence 3F soit 660 Hz, ce qui donne après addition
- d'un peu de La 4 simple, la 3ème harmonique, l'octave 2 : fréquence 4F soit 880 Hz, ce qui donne après addition
- d'un peu de Do# 5 simple : la 4ème harmonique, la tierce : fréquence 5F soit 1100 Hz, ce qui donne finalement
- d'un peu de Mi 5 simple : la 5ème harmonique, la quinte 2... etc.....
La façon dont chacun de ces 'un peu' est ajusté par rapport à ses copains caractérise justement l'instrument.
Si on joue un La 3 sur une guitare, il est composé des mêmes harmoniques que l'orgue, mais pas avec la même répartition. Par exemple pour l'orgue, la 4ème harmonique sera seulement les 6 % de la fondamentale, alors que pour la guitare, la 4ème harmonique sera les 27 % de la fondamentale. (J'en sais rien, ch'uis pas sûr, je dis n'importe quoi, c'est un exemple...).
C'est sur ce raisonnement génial qu'ont été construit les premiers synthétiseurs.
On demande d'abord à l'oscillateur de produire un son simple tout con : une sinusoïde de 220 Hz. Ça fait beep, c'est moche mais ça marche.
On lui demande ensuite de produire à la fois une sinusoïde de 220 Hz et en même temps une autre de 440 Hz mais moitié moins fort. Ça fait un autre beep à peine moins con.
Alors on complique, on ajoute des harmoniques selon diverses répartitions, et le beep devient de plus en plus riche. Et si on prend une répartition plutôt qu'une autre, on arrive à faire un son qui rappelle soit un instrument à vent (orgue), soit un instrument à corde (violon), soit un instrument... hum !
Tout ça participe au TIMBRE de l'instrument.
Bien sûr, il faut rajouter plein d'autres trucs pour imiter le vrai instrument :
- des bruits de jeu : le gratouillis du doigt sur la corde de la guitare ou le choc du marteau pour le piano, ou l'ouverture de la porte du registre pour le tuyau d'orgue
- faire évoluer le son au cours du temps : le son d'orgue est quasi-constant durant le maintien du doigt sur la touche, alors que le son du piano diminue assez vite.
Mais FOURIER, le pôvre, il avait pas Windows 95 (Windows 1793 n'était pas encore sorti !) ni Cubase, alors il savait pas qu'on pouvait se faire chier des heures avec des supers bugs au lieu de jouer de la musique peinard sur son luth à pédale !
ADDITION D'ONDES SONORES

D'abord, une onde sonore simple, ça se représente par une sinusoïde. Qu'est-ce que ça signifie ? Eh bien par exemple regarde la courbe bleue ci-contre. C'est une sinusoïde. Imagine que le temps qui passe se déroule dans le sens de la ligne noire horizontale autour de laquelle se déploie la sinusoïde.
| 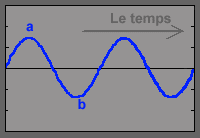
Nota : La courbe monte-descend-et-remonte. On appelle "longueur d'onde" la distance que le son a parcouru pendant ce temps là.
|
A un moment donné, la courbe est au-dessus de cet axe du temps (a), un peu plus tard elle est au-dessous (b), et cela alternativement et régulièrement, 220 fois par secondes si le son est un La à 220
Hz.
Maintenant, que veut dire additionner deux sons ?

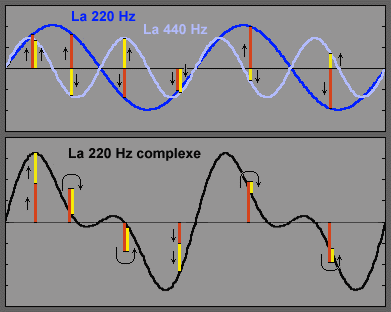
Dans la figure ci-dessous, la sinusoïde bleue représente par exemple un La de 220 Hz et la sinusoïde bleu clair, le La à l'octave, de 440 Hz. Tu remarques que la 2ème monte-descend-et-remonte deux fois plus vite que la 1ère. C'est parce que c'est un son plus aigu ! L'addition de ces 2 ondes donne l'onde noire inférieure. Pourquoi a-t-elle une forme plus complexe que les simples sinusoïdes précédentes ? C'est parce que cette forme est le résultat de l'addition point par point des deux courbes. Pour quelques points particuliers, j'ai mis en haut un segment rouge qui montre la hauteur de la 1ère courbe et un segment jaune qui montre la hauteur de la 2ème courbe. Par simple addition, quand les 2 segments sont dans le même sens, ils s'ajoutent, vers le haut ou vers le bas. S'ils sont dans des sens opposés, ils se retranchent. Tout simplement !
Le son résultant est encore un autre La à 220 Hz car sa longueur d'onde principale (fondamentale) reste identique au La 220 Hz d'origine. Compare la courbe noir à la courbe bleu-foncé : l'intervention du 2ème La à 440 Hz (le 1er harmonique) a modifié simplement la forme de la courbe bleue, la fondamentale
Guy COULON, le 17-12-1998

Page vue 24684 fois




