Rechercher

- "Tu vois mon fils, cette bouteille de lait a été spécialement conçue pour une ergonomie maximale et particulièrement pour l'utilisation par des..."

- "Et comment on fait les bébés ?"

- "... Bon, d'accord, tu l'auras voulu."

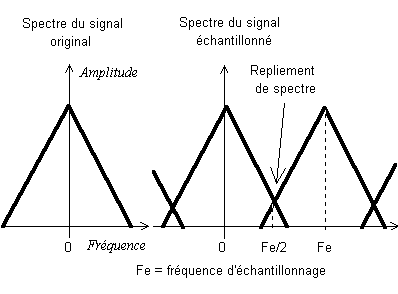
Parlons d'abord du CAN. Tu sais (?) qu'en échantillonnant à une fréquence donnée, disons 48 kHz, il ne faut pas que les signaux d'entrée aient des fréquences supérieures à 24 kHz (théorème de Shannon ou critère de Nyquist selon les écoles, déjà évoqué sur le site). Toutes les fréquences supérieures à ce seuil se "replient", c'est-à-dire que d'inaudibles, elles deviennent audibles après échantillonnage...

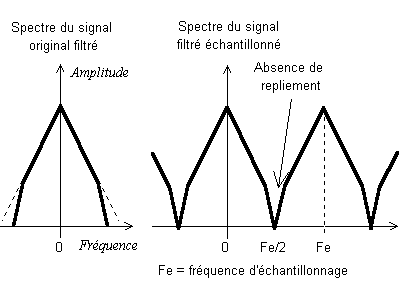
De ce fait, tout CAN qui se respecte, doit être muni d'un filtre passe-bas avant échantillonnage afin de couper les fréquences en question. (en fait, il suffit d'atténuer ces fréquences de façon qu'elle passent en dessous du pas de quantification du CAN).

Ce filtre passe-bas doit impérativement être réalisé en analogique puisqu'on échantillonne après, et c'est là le problème... Il est très difficile de faire un filtre à la fois :

Avec un CAN 48 kHz et une bande passante de 20 kHz, il ne reste que 4 kHz pour couper ce qui pourrait gêner. Je rappelle qu'un CAN 16 bits a de l'ordre de 90dB de dynamique, il faudrait atténuer de quelque chose comme 90 dB entre 20 et 24 kHz !!!! (filtre d'ordre ??? 20kHz / 4kHz x 90 dB / 12 dB/oct. = 37.5 ???, ho non, j'm'a trompé, pas possible ??? ça c'est ma température au lever du jour !!!) Je n'épiloguerai pas sur le cas d'un échantillonnage à 22 kHz pour lequel on est obligé de couper en dessous de 11 kHz...

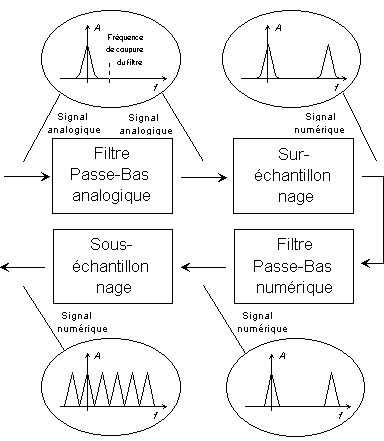
D'où la ruse suivante motivée par d'autres astuces de traitement des signaux que je ne développerai pas : on va échantillonner largement au-dessus de ce dont on a besoin, disons 128 fois plus haut (48 kHz x 128 =... beaucoup, > 5 MHz). Et alors, on a 127 x 24 kHz de bande pour atténuer d'un facteur environ 90 dB, ouf, on prend un peu d'air... même beaucoup ! Un passe-bas de base suffit alors. Oui, mais on voulait du 48 kHz, parce que là, même avec 256 Mo de RAM, on va pas faire long feu.

Il faut donc sous-échantillonner numériquement le signal d'un facteur 128 - numériquement parce qu'on a déjà échantillonné, ce qui pose à nouveau le problème du repliement des fréquences. On ajoute alors un passe-bas cette fois numérique, qui filtre entre 20 et 24 kHz, sans déphasage en-dessous de 20kHz, avec une réponse ultra plate entre 0 et 20 kHz (vive le numérique), et surtout, pour le prix de quelques mm² de silicium, donc pas grand chose. Et le tour est joué ! Y'a plus qu'à prendre un point sur 128, et on a du (très bon) 48 kHz / 16 bits.

Enfin à titre exhaustif, sache que le fait de sur-échantillonner apporte trois avantages :

Le point 3 a quand même comme conséquence fâcheuse que le nombre de bits de sortie n'est pas directement lié au niveau de bruit du numérique (le bruit de quantification). En effet, ce n'est pas parce qu'on filtre sur 32 bits que le bruit équivaut à un CAN 32 bits, VST le prouve ! Méfiance donc à la lecture des caractéristiques...

T'as tout pigé ?

Bon ben alors, passons au CNA. CNA, CAN même combat ! Toujours le duo infernal Shannon / Nyquist. Lorsqu'on restitue un signal échantillonné (je garde mon 48 kHz, c'est plus facile à taper que 44.1), on périodise le spectre (!!!!). C'est exactement le contraire de l'opération précédente, avant les fréquences inaudibles devenaient audibles, maintenant celles audibles deviennent inaudibles... Les fréquences qu'on a entre 0 et 24 kHz, et ben elles génèrent la même chose entre 24 et 48, 48 et 72, 72 et 96 etc. C'est pas trop gênant à 48 kHz, mais si vous utilisez du 22 kHz, ça le devient, et ça s'appelle l'aliasing.

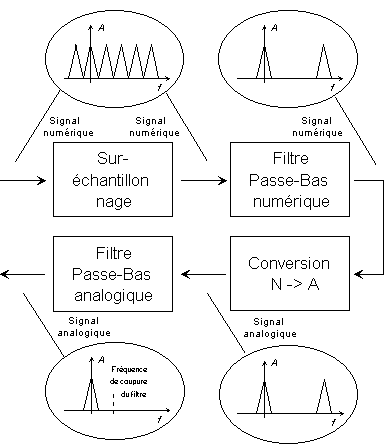
Donc le signal restitué ne ressemble pas à celui échantillonné : il est fait de marches d'escalier, alors que celui de départ était tout lisse. Si on veut couper tout ce qui n'appartient pas au signal d'origine, il faut encore filtrer passe-bas, très raide, un chouïa au-dessus de 24 kHz... (et ce serait au-dessous de 11 kHz pour du 22 kHz pour ceux qui ont suivi, la moitié quoi). On fait donc appel à un sur-échantillonnage numérique préalable (allez, un p'tit x 128), suivi d'un filtrage numérique pour éliminer les indésirables (fastoche, 1 mm² de silicium en plus et hop !). Le spectre est alors vide entre 24 kHz et 24 kHz * 128...

Il ne reste plus qu'à convertir en analogique et appliquer un filtre passe-bas analogique (de base) pour les fréquences qui dépasseraient 24 kHz x 128 =..., facile non ? Je suis sûr que tu as déjà vu sur un lecteur de CD une histoire de "sur-échantillonnage N fois", c'est de cela dont il s'agit !

Résumé :

La séance de torture est terminée, vous pouvez reprendre une activité normale et saine !

Jean-Michel PHILIPPE, le 05-04-2000

Page vue 33443 fois