Search this Site



Fourier Analysis

You're here : Audio >Learning

From the mathematician Joseph Fourier (18 th century) not to be mistaken with Charles Fourier (same period but "Fourierism" theorician, the forerunner of "communism").

Roughly, Joseph demonstrates that any MUSICAL sound (therefore, not noises), COMPLEX (therefore, not simple), with a frequency F, can be divided into an addition of SIMPLE sounds (sinusoid : a sound produced by a mere oscillator, a beep) with their HARMONICS with a frequency 2F then 3F, 4F....

In other words, if we play a simple A2 on an organ, it's composed of :

The way all these "little bits" are adjusted with their little friends actually determines an instrument's characteristics.

If we play an A3 on a guitar, it's composed of the same harmonics as the organ but not with the same distribution. For example with the organ, the fourth harmonic will only be 6 % of the tonic, whereas on the guitar, the fourth harmonic will be 27 % of the tonic. ( I don't know, I'm not sure, I said anything, it's just an example...)

The first synthesizers were built following this fantastic thought process.

We ask the oscillator to make a simple silly sound, a 220 hz sinusoid. It is a Beep, it sounds awful but it works.

Then it is asked to produce simultaneously a 220-hz sinusoid plus another one at 440 hz but half stronger. It makes another beep barely silly.

Then we complicate, we add harmonics, follwing various distributions and the beep becomes richer and richer. And if we take one distribution rather than another one, we manage to produce a sound reminding us of a wind instrument (organ), or a string instrument (violin), or an instrument....Hum !

All of this makes the instrument's TONE.

Of course we have to add lots of things to imitate the real instrument.
  • Sound produced while playing : finger noises on the guitar strings or the impact of piano hammers, or the opening of the register-door for the organ's pipe.
  • Change the sound over time : the sound of the organ is fairly constant when maintaining the finger on the key, whereas the sound of the piano dicreases quickly.

But Fourier, poor man, didn't have Windows 95 ( Windows 1793 wasn't published yet ! ) or Cubase, so he didn't know that one could put themselves out during hours with wonderfull bugs instead of playing music calmly on his "pedal-lute" !

ADDITION OF SOUND WAVE

First, a simple sound wave, represented by a sinusoid. What does it mean ? For example, look at the blue curve beside. It's a sinusoid. Imagine that time passes along the horizontal black line around which the sinusoid is represented.

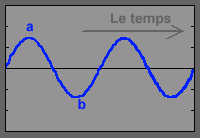
Note : the curve "goes up and down and up". We call "wavelength" the distance covered by the sound during this time.

At a certain point, the curve is above this axis (a), later it is below (b), and this alternately and regularly, 220 times per second if the sound is a 220-Hz A.

And now, what does "adding two sounds" mean ?

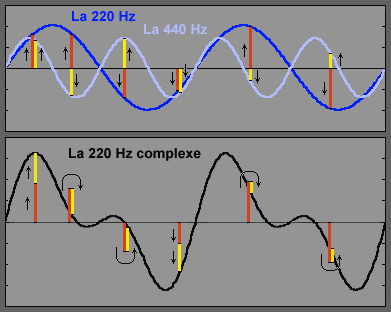
In the picture above, the blue sinusoid is for example a 220-Hz Aand the light blue sinusoid, the 440-Hz A, the octave. . You'll notice that the second curve goes up and down and up twice faster than the first one. It's because it is a higher-pitched sound ! The addition of these two waves makes the black wave below. Why does it have a more complex shape than the first simple sinusoids ? It's because this one is the addition, point by point, of the two curves. For some particular points I've made red segments which show the first curve's height and a yellow segment for the second curve's height. By simple addition when both segments are in the same direction, they add to each other, upward or downward . When they are opposed they substract from each other. It's all that simple !

The result is another 220-Hz A because his main wavelength (tonic) is the same as the original 220-Hz A. Compare the black curve and the dark blue curve : the action of the second 440-Hz A (the first harmonic) simply modified the blue curve's shape, the tonic.

Guy COULON, on the 17-12-1998
Page viewed 9145 times