Search this Site



Periodic Sounds

You're here : Audio >Learning

Periodic sounds are those you can use to write a melody (as opposed to noises and percussions).

Sinusoidal sounds : we can't find them like this in nature but we use them to analyse real sounds. Indeed, almost all real sounds are periodic. They are generated by the vibration of a sonic material (reeds, strings, airstreams etc...) and can be split up into a sum of several sinusoidal sounds.

FOURIER mathematically demonstrated that any periodic oscillation can be split up into a sum of sinusoidal oscillations according to a rule called FOURIER'S LAW.

Simple sinusoidal sound (for instance, the 440 Hz "A" you can hear when you pick up the phone !). Its mathematical representation is :

X=Asin(2p f t)

Where X represents a vibrating point on the sonic material ( a spot on a string, the displacement of an air molecule), A the amplitude of sound, f the frequency and t the time.

FOURIER thus demonstrated that a periodic phenomenon (a sound) was alaways the result of the superimposition of several simple sinusoidal waves of which frequencies were a mutiple of the original frequency.

Example : let's take a C1, the frequency of which is 65 Hz. The series of resulting harmonic frequencies will be the following : 65, 130, 195, 260, ..., ... n times 65

And it is the sum of all these resulting sounds which will produce a complex sinusoidal sound.

Its mathematical expression will be the following :

X=A1sin(2pf t)+ A2sin(2p2f t)+ A3sin(2p3f t)+ A4sin(2p4f t))+ ... and so on to infinity...

We can have any value. Yet, we wil notice that, most of the time, this value decreases in proportion to n.

This function allows us to generate any periodic sound and the values of A1..........An will determine the sound tone.

Important note : real sounds, that is to say those generated by real instruments, do not completely follow this rule, and the first synthesizers, which strictly followed this principle, never satisfied a trained ear !

A few examples

(Click on the pictures to listen to the sounds)

Pure sinusoidal sound

Sawtooth signal : the whole series of harmonics is used (Violin).

Square sound : only even harmonics are used.

Synthetic violin sound, C4 or DO3 at 262 Hz.

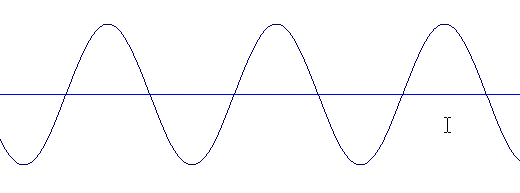
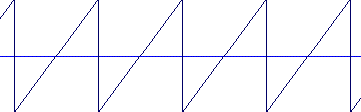
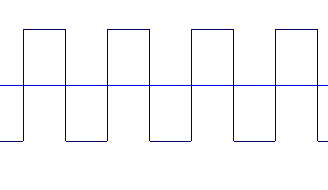
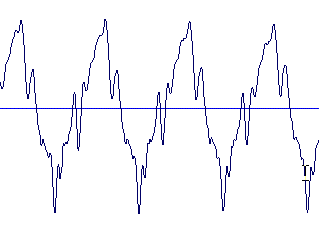
Let's notice that the pure sinusoidal sound seems to have a lower definition in high frequencies and that the square signal seems to be higher-pitched than the sawtooth signal.

A very good tool allows us to understand a sound's spectral and harmonic content and then to represent its structure graphically : the sonograph.

Bruno CANADAS, on the 05-04-2000
Page viewed 10966 times