Phase shift
Electrically speaking, the mixing of the two signals is achieved by adding their gain at each point in time. For instance, at a given point in time, one signal’s gain is +10, the other’s is –15, the resulting signal thus having a gain of –5. Within a mixing board, for two signals to be fully mixed their pan settings have to be exactly the same. On the other hand, if they’re panned one to hard left, the other to hard right, they’ll stay independent one from the other because they’ll take different "paths" or "busses".
The red curve is the original signal, the blue one is the signal that has been phase-shifted; in black, the result of adding these two.
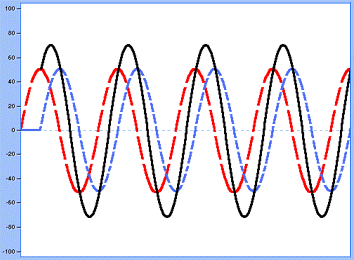
In the present case, the phase shift amount to about 1/4 of a period, the final wave displays increased amplitude, but for another signal the result might be totally different. Let’s study another case :
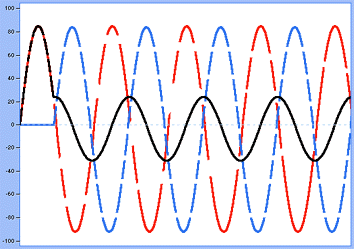
Now, that changes everything ! Here, the resulting signal has less amplitude than the original ones, because the two waves are almost always opposite one to the other and partly cancel each other. We can observe that the relationship between the duration of the delay (phase shift) and the period of the original sine wave is an important parameter, some waves will be almost unaffected, others quite drastically by such a treatment. When the delay is equal to half the period of the original signal, the two waves fully cancel each other; I’ll let you draw it, you’ll see, it’s easy.
Of course, for us it’s a bit more complex and sounds conveyed through a mixing desk rarely are pure sine waves, or perhaps only for scientific uses. The music of ours is made of complex sounds, i.e. myriads of sine waves with different frequencies. To this (which is true for the “sustained” sounds) should be added attacks, which often have little relationship with the played note, but more often with the instrument itself.
So, when summing two identical signals, one phase-shifted a few milliseconds vs. the other, some frequencies will be amplified, some others will be attenuated. Low frequencies having very long periods will be hardly attenuated, or the delay would have to be so long that it would become noticeable, so they are virtually immune to this treatment. The higher in the frequency spectrum, the more noticeable the changes in the resulting sound. A frequency (and its harmonics) will be amplified, another will be fully cancelled. From a spectral standpoint the result is a series of "holes" and "bumps" and we will obtain what’s called a "comb filter".
The one on the diagram below is exaggerated on purpose (to better see it ;-) The horizontal axis is signal’s frequency in hertz and the vertical axis is the filter’s gain in decibels.
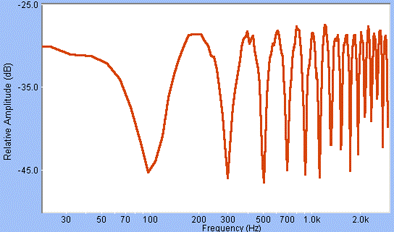
The greater the delay between the two signals, the more the “comb effect” will start in the lower frequencies. For a full cancellation of a sine wave, the delay has to be equal to half the period of the wave. With a 0.1ms delay, the first frequency to be cancelled has a period of 0.2ms, i.e. a frequency of 5000Hz, whereas a sine with a 10kHz frequency would see its amplitude doubled since its delayed image would exactly match the original (the two being called “in phase”). This comb filter effect is found in… phasing, flanging...
Now a quick case study: take a delay effect, of which you set the feedback ratio to 0%, have a sound go through it, mixed 1:1 with the original, manually sweep the delay amount between 0 and 10ms, and listen!
During a live take, wavelength has to be taken into account. Wavelength is the “size” of a period of the signal, and the formula to compute it is :
where 
(lambda) is the wavelength in meters, 340 the speed of sound in air at 20°C, and F the frequency of that sound. If you put two mikes pointing in the same direction, but not at the same distance from the source of sound, the adverse effects of comb filtering will appear as you move one of the mikes back- or forward… Welcome to the world of home phase-shifting !!
Hey, what a minute ! So, what’s "inverting phase", now ?
In this specific case, the signal is not really delayed, but its polarity is inverted, i.e. "+" becomes "-", all positive values in the signal become negative and vice-versa. Two identical sounds thus added will fully and perfectly cancel each other. This case is only possible electrically. The diagram below shows a signal (red), its image with inverted phase (blue), when one is at +10dB the other is a –10dB, and the result is the black signal… Pure silence!
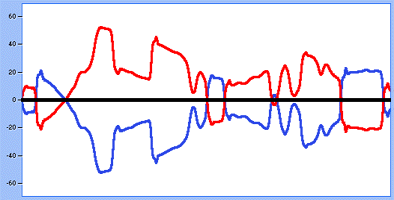
From an acoustic standpoint, the closest equivalent is recording a snare drum with two mikes directed to the same point and at the same distance but in opposite direction. Everything positive in one mike will be negative in the other… If you don’t invert phase in the mixer channel of one of these mikes, your speakers won’t deliver much, or perhaps quite a strange sound, all parts common to the two mikes will be cancelled (if panned the same). If the signals coming from the mikes are panned one hard left and the other hard right, phase cancellation will take place in the speakers, when the membrane of one moves forward, the other moves backward. Phase shift will then be transmitted acoustically.
Now back to a temporal shift (still with hard left and right panning), if both speakers are at equal distance from your ears, then your brain will perceive the delay and will render it as information about… spatialization!! Which we will study later on !